Simple Matrix Inversion in Pure Python without Numpy or Scipy
To Help with Insight and Future Research Tools
Get it on GitHub AND check out Integrated Machine Learning & AI coming soon to YouTube.
Overview
We will be walking thru a brute force procedural method for inverting a matrix with pure Python. Why wouldn’t we just use numpy or scipy? Great question. This blog is about tools that add efficiency AND clarity. I love numpy, pandas, sklearn, and all the great tools that the python data science community brings to us, but I have learned that the better I understand the “principles” of a thing, the better I know how to apply it. Plus, tomorrows machine learning tools will be developed by those that understand the principles of the math and coding of today’s tools.
Also, once an efficient method of matrix inversion is understood, you are ~ 80% of the way to having your own Least Squares Solver and a component to many other personal analysis modules to help you better understand how many of our great machine learning tools are built. Would I recommend that you use what we are about to develop for a real project? All those python modules mentioned above are lightening fast, so, usually, no. I would not recommend that you use your own such tools UNLESS you are working with smaller problems, OR you are investigating some new approach that requires slight changes to your personal tool suite. Thus, a statement above bears repeating: tomorrows machine learning tools will be developed by those that understand the principles of the math and coding of today’s tools. I want to be part of, or at least foster, those that will make the next generation tools. Plus, if you are a geek, knowing how to code the inversion of a matrix is a great right of passage! We will also go over how to use numpy /scipy to invert a matrix at the end of this post.
The way that I was taught to inverse matrices, in the dark ages that is, was pure torture and hard to remember! If you go about it the way that you would program it, it is MUCH easier in my opinion. I would even think it’s easier doing the method that we will use when doing it by hand than the ancient teaching of how to do it. In fact, it is so easy that we will start with a 5×5 matrix to make it “clearer” when we get to the coding.
DON’T PANIC. The only really painful thing about this method of inverting a matrix, is that, while it’s very simple, it’s a bit tedious and boring. However, compared to the ancient method, it’s simple, and MUCH easier to remember. Or, as one of my favorite mentors would commonly say, “It’s simple, it’s just not easy.” We’ll use python, to reduce the tedium, without losing any view to the insights of the method.
The Math
Let’s start with some basic linear algebra to review why we’d want an inverse to a matrix.
Consider a typical linear algebra problem, such as:
AX=B,\hspace{5em}\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{bmatrix}\begin{bmatrix}x_{11}\\x_{21}\\x_{31}\end{bmatrix}=\begin{bmatrix}b_{11}\\b_{21}\\b_{31}\end{bmatrix}We want to solve for X, so we obtain the inverse of A and do the following:
X=A^{-1}B,\hspace{5em} \begin{bmatrix}x_{11}\\x_{21}\\x_{31}\end{bmatrix} =\begin{bmatrix}ai_{11}&ai_{12}&ai_{13}\\ai_{21}&ai_{22}&ai_{23}\\ai_{31}&ai_{32}&ai_{33}\end{bmatrix}\begin{bmatrix}b_{11}\\b_{21}\\b_{31}\end{bmatrix}Thus, we have a motive to find A^{-1}. So how do we easily find A^{-1} in a way that’s ready for coding? Let’s start with the logo for the github repo that stores all this work, because it really says it all:
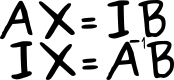
We frequently make clever use of “multiplying by 1” to make algebra easier. One way to “multiply by 1” in linear algebra is to use the identity matrix. In case you’ve come here not knowing, or being rusty in, your linear algebra, the identity matrix is a square matrix (the number of rows equals the number of columns) with 1’s on the diagonal and 0’s everywhere else such as the following 3×3 identity matrix.
I= \begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}Following the main rule of algebra (whatever we do to one side of the equal sign, we will do to the other side of the equal sign, in order to “stay true” to the equal sign), we will perform row operations to A in order to methodically turn it into an identity matrix while applying those same steps to what is “initially” the identity matrix. When what was A becomes an identity matrix, I will then be A^{-1}. It’s important to note that A must be a square matrix to be inverted. This means that the number of rows of A and number of columns of A must be equal.
If at some point, you have a big “Ah HA!” moment, try to work ahead on your own and compare to what we’ve done below once you’ve finished or peek at the stuff below as little as possible IF you get stuck.
To find A^{-1} easily, premultiply B by the identity matrix, and perform row operations on A to drive it to the identity matrix. You want to do this one element at a time for each column from left to right.
AX=IB,\hspace{5em}\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{bmatrix}\begin{bmatrix}x_{11}\\x_{21}\\x_{31}\end{bmatrix}= \begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix} \begin{bmatrix}b_{11}\\b_{21}\\b_{31}\end{bmatrix}Perform the same row operations on I that you are performing on A, and I will become the inverse of A (i.e. A^{-1}).
IX=A^{-1}B,\hspace{5em} \begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix} \begin{bmatrix}x_{11}\\x_{21}\\x_{31}\end{bmatrix} =\begin{bmatrix}ai_{11}&ai_{12}&ai_{13}\\ai_{21}&ai_{22}&ai_{23}\\ai_{31}&ai_{32}&ai_{33}\end{bmatrix}\begin{bmatrix}b_{11}\\b_{21}\\b_{31}\end{bmatrix}Here are the steps, S, that we’d follow to do this for any size matrix. This is just a high level overview. We’ll do a detailed overview with numbers soon after this. Think of the inversion method as a set of steps for each column from left to right and for each element in the current column, and each column has one of the diagonal elements in it, which are represented as the S_{k1} diagonal elements where k=1\, to\, n. We’ll start with the left most column and work right. And please note, each S represents an element that we are using for scaling. When we are on a certain step, S_{ij}, where i \, and \, j = 1 \, to \, n independently depending on where we are at in the matrix, we are performing that step on the entire row and using the row with the diagonal S_{k1} in it as part of that operation.
S = \begin{bmatrix}S_{11}&\dots&\dots&S_{k2} &\dots&\dots&S_{n2}\\S_{12}&\dots&\dots&S_{k3} &\dots&\dots &S_{n3}\\\vdots& & &\vdots & & &\vdots\\ S_{1k}&\dots&\dots&S_{k1} &\dots&\dots &S_{nk}\\ \vdots& & &\vdots & & &\vdots\\S_{1 n-1}&\dots&\dots&S_{k n-1} &\dots&\dots &S_{n n-1}\\ S_{1n}&\dots&\dots&S_{kn} &\dots&\dots &S_{n1}\\\end{bmatrix}If at this point you see enough to muscle through, go for it! Then come back and compare to what we’ve done here.
The Generalized Order of Steps
We’ll call the current diagonal element the focus diagonal element, or fd for short. The first step (S_{k1}) for each column is to multiply the row that has the fd in it by 1/fd. We then operate on the remaining rows (S_{k2} to S_{kn}), the ones without fd in them, as follows:
- use the element that’s in the same column as fd and make it a multiplier;
- replace the row with the result of … [current row] – multiplier * [row that has fd], and do this operation to the I matrix also.
- this will leave a zero in the column shared by fd in the A matrix.
We do this for all columns from left to right in both the A and I matrices. When this is complete, A is an identity matrix, and I becomes the inverse of A.
Let’s go thru these steps in detail on a 3 x 3 matrix, with actual numbers. We start with the A and I matrices shown below. Then, code wise, we make copies of the matrices to preserve these original A and I matrices, calling the copies A_M and I_M.
Our starting matrices are:
A=\begin{bmatrix}5&3&1\\3&9&4\\1&3&5\end{bmatrix}\hspace{5em} I=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}
A_M and I_M , are initially the same, as A and I, respectively:
A_M=\begin{bmatrix}5&3&1\\3&9&4\\1&3&5\end{bmatrix}\hspace{4em} I_M=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}
1. Using the steps and methods that we just described, scale row 1 of both matrices by 1/5.0
A_M=\begin{bmatrix}1&0.6&0.2\\3&9&4\\1&3&5\end{bmatrix}\hspace{5em} I_M=\begin{bmatrix}0.2&0&0\\0&1&0\\0&0&1\end{bmatrix} 2. Subtract 3.0 * row 1 of A_M from row 2 of A_M, and
Subtract 3.0 * row 1 of I_M from row 2 of I_M
3. Subtract 1.0 * row 1 of A_M from row 3 of A_M, and
Subtract 1.0 * row 1 of I_M from row 3 of I_M
4. Scale row 2 of both matrices by 1/7.2
A_M=\begin{bmatrix}1&0.6&0.2\\0&1&0.472\\0&2.4&4.8\end{bmatrix}\hspace{5em} I_M=\begin{bmatrix}0.2&0&0\\-0.083&0.139&0\\-0.2&0&1\end{bmatrix}5. Subtract 0.6 * row 2 of A_M from row 1 of A_M
Subtract 0.6 * row 2 of I_M from row 1 of I_M
6. Subtract 2.4 * row 2 of A_M from row 3 of A_M
Subtract 2.4 * row 2 of I_M from row 3 of I_M
7. Scale row 3 of both matrices by 1/3.667
A_M=\begin{bmatrix}1&0&-0.083\\0&1&0.472\\0&0&1\end{bmatrix}\hspace{5em} I_M=\begin{bmatrix}0.25&-0.083&0\\-0.083&0.139&0\\0&-0.091&0.273\end{bmatrix}8. Subtract -0.083 * row 3 of A_M from row 1 of A_M
Subtract -0.083 * row 3 of I_M from row 1 of I_M
9. Subtract 0.472 * row 3 of A_M from row 2 of A_M
Subtract 0.472 * row 3 of I_M from row 2 of I_M
It all looks good, but let’s perform a check of A \cdot IM = I.
A \cdot IM=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}Yes! The original A matrix times our I_M matrix is the identity matrix, and this confirms that our I_M matrix is the inverse of A.
The Code
I want to encourage you one last time to try to code this on your own. Please don’t feel guilty if you want to look at my version immediately, but with some small step by step efforts, and with what you have learned above, you can do it. If you get stuck, take a peek, but it will be very rewarding for you if you figure out how to code this yourself.
When you are ready to look at my code, go to the Jupyter notebook called MatrixInversion.ipynb, which can be obtained from the github repo for this project. You don’t need to use Jupyter to follow along. I’ve also saved the cells as MatrixInversion.py in the same repo. Let’s first define some helper functions that will help with our work.
There are also some interesting Jupyter notebooks and .py files in the repo. I encourage you to check them out and experiment with them. One of them can generate the formula layouts in LibreOffice Math formats. If you don’t use Jupyter notebooks, there are complementary .py files of each notebook.
Let’s first introduce some helper functions to use in our notebook work. PLEASE NOTE: The below gists may take some time to load.
NOTE: The last print statement in print_matrix uses a trick of adding +0 to round(x,3) to get rid of -0.0’s. Try it with and without the “+0” to see what I mean.
Let’s prepare some matrices to use.
As previously stated, we make copies of the original matrices:
Let’s run just the first step described above where we scale the first row of each matrix by the first diagonal element in the A_M matrix.
Now, we can use that first row, that now has a 1 in the first diagonal position, to drive the other elements in the first column to 0.
Let’s simply run these steps for the remaining columns now:
That completes all the steps for our 5×5. I_M should now be the inverse of A. Let’s check that A \cdot I_M = I .
Success! A_M has morphed into an Identity matrix, and I_M has become the inverse of A. Yes! When we multiply the original A matrix on our Inverse matrix we do get the identity matrix.
I do love Jupyter notebooks, but I want to use this in scripts now too. See the code below. This is the last function in LinearAlgebraPurePython.py in the repo. It is imported and implemented by LinearAlgebraPractice.py. Note there are other functions in LinearAlgebraPurePython.py being called inside this invert_matrix function. Note that all the real inversion work happens in section 3, which is remarkably short. The other sections perform preparations and checks.
def invert_matrix(A, tol=None):
"""
Returns the inverse of the passed in matrix.
:param A: The matrix to be inversed
:return: The inverse of the matrix A
"""
# Section 1: Make sure A can be inverted.
check_squareness(A)
check_non_singular(A)
# Section 2: Make copies of A & I, AM & IM, to use for row ops
n = len(A)
AM = copy_matrix(A)
I = identity_matrix(n)
IM = copy_matrix(I)
# Section 3: Perform row operations
indices = list(range(n)) # to allow flexible row referencing ***
for fd in range(n): # fd stands for focus diagonal
fdScaler = 1.0 / AM[fd][fd]
# FIRST: scale fd row with fd inverse.
for j in range(n): # Use j to indicate column looping.
AM[fd][j] *= fdScaler
IM[fd][j] *= fdScaler
# SECOND: operate on all rows except fd row as follows:
for i in indices[0:fd] + indices[fd+1:]:
# *** skip row with fd in it.
crScaler = AM[i][fd] # cr stands for "current row".
for j in range(n):
# cr - crScaler * fdRow, but one element at a time.
AM[i][j] = AM[i][j] - crScaler * AM[fd][j]
IM[i][j] = IM[i][j] - crScaler * IM[fd][j]
# Section 4: Make sure IM is an inverse of A with specified tolerance
if check_matrix_equality(I,matrix_multiply(A,IM),tol):
return IM
else:
raise ArithmeticError("Matrix inverse out of tolerance.")
I hope that you will make full use of the code in the repo and will refactor the code as you wish to write it in your own style, AND I especially hope that this was helpful and insightful.
It’s interesting to note that, with these methods, a function definition can be completed in as little as 10 to 12 lines of python code. This type of effort is shown in the ShortImplementation.py file. I don’t recommend using this. The shortest possible code is rarely the best code. But it is remarkable that python can do such a task in so few lines of code.
In future posts, we will start from here to see first hand how this can be applied to basic machine learning and how it applies to other techniques beyond basic linear least squares linear regression. However, we may be using a closely related post on “solving a system of equations” where we bypass finding the inverse of A and use these same basic techniques to go straight to a solution for X.
Matrix Inversion with Numpy / Scipy
It’s a great right of passage to be able to code your own matrix inversion routine, but let’s make sure we also know how to do it using numpy / scipy from the documentation HERE. See if you can code it up using our matrix (or matrices) and compare your answer to our brute force effort answer. My approach using numpy / scipy is below.
After you’ve read the brief documentation and tried it yourself, compare to what I’ve done below:
import numpy as np from numpy.linalg import inv a = np.array([[5., 3., 1.], [3., 9., 4.], [1., 3., 5.]]) print(a, '\n') ainv = inv(a) ainv = ainv.round(3) print(ainv)
Notice the round method applied to the matrix class. Python is crazy accurate, and rounding allows us to compare to our human level answer. Below is the output of the above script.
[[5. 3. 1.]
[3. 9. 4.]
[1. 3. 5.]]
[[ 0.25 -0.091 0.023]
[-0.083 0.182 -0.129]
[ 0. -0.091 0.273]]The first matrix in the above output is our input A matrix. The second matrix is of course our inverse of A.
Closing Remarks
If you did most of this on your own and compared to what I did, congratulations! I know that feeling you’re having, and it’s great! If you didn’t, don’t feel bad. There will be many more exercises like this to come. My encouragement to you is to make the key mathematical points your prime takeaways. The main thing to learn to master is that once you understand mathematical principles as a series of small repetitive steps, you can code it from scratch and TRULY understand those mathematical principles deeply. Doing such work will also grow your python skills rapidly. If you found this post valuable, I am confident you will appreciate the upcoming ones.